Strip Load Surcharge Analysis using Elastic Methods

UPDATED – Problem Solved…

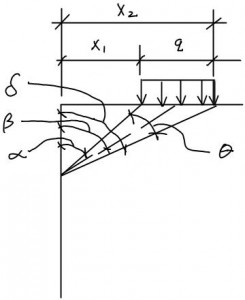
Here we will dig deeper into analyzing strip loads with elastic methods. First to avoid confusion between seeing similar equations which use different reference angles, we will set our own nomenclature.

Nomenclature

K = Constant typically between 1 and 2, depending on the stiffness of the wall. It may be appropriate to use K=1 for flexible walls such as cantilevered sheet pile, segmental walls. It may be appropriate to use K=2 for rigid walls. Refer to CivilTech Software manual (http://www.civiltechsoftware.com/downloads/sh_manu.pdf).

 

Below are (2) common equations which result in the same solution but are shown differently. I will refer to these equations as the integrated method or equations. Most codes and design guides refer to these equations but it seems too differ on who is credited. Some refer to them as Boussinesq as modified by Tang or Spangler, others Mindlin or Terzaghi (although Terzaghi is mostly responsible for modifying point and line load elastic equations).

Note that β is located at half of θ and not half the width of the strip load.

The other

In Joseph Bowles’ “Foundation Analysis and Design” he discuses different methods of analyzing offset surcharges using elastic methods. He discuss the work of Spangler and the factor of two suggested by Mindlin. In summary he suggests that Spangler’s experiments were not accurate and possibly flawed due to the setup geometry. Also the equations derived by Spangler use a Poisson’s ratio of 0.5 which may not be correct for all soils. However Spangler’s equation for the strip load results in the same equation as shown above. Bowles also states that Mindlins reasoning for the factor 2 (Mindlin says that a rigid wall produced a mirror effect) is wrong.
Bowles suggests to only use the original Boussinesq equation.

[EQN – 1]

With these equations one can “discretize” the strip load. Meaning you divide the strip load into a series of concentrated loads. Then apply the Boussinesq equation to each point load. Then the sum the results to find the resulting pressure at a certain elevation on the wall. You then find these resulting pressures at a certain number of elevations on the wall and sum these to find the resulting total force. It should be noted that Poisson’s ratio should be modified so that it represents a plan strain condition.

where represents a triaxial condition
Refer to Excavating Systems, Planning, Design and Safety, 2009 for the following suggested values of
Moist clay soils: 0.4-0.5
Saturated clay soils: 0.45-0.5
Cohesionless, medium dense: 0.3-0.4
Cohesionless, loose to medium: 0.2-0.35

Here are some notes on the discretized method (semi-large file – about 10MB, I will try to shrink later):
Boussinesq Strip Load Discritization Method 2

Now my problem is this – when I compare the “discretized” approach to the integrated I do not get similar values, not even close. I have to think that I am in error somewhere, but I cannot find where. I have compared spreadsheets to other programs to hand calcs. I will continue to search, but for now, I have attached a couple hand calcs showing the discrepancy. I will also attach a spreadsheet comparing techniques.

UPDATE:

I believe I have now solved this problem. Where I went wrong – When integrating for a strip load you would use boundary conditions from +infinity to -infinity. Which is NOT what I was doing. I was taking the load as if it was an AREA surcharge over a one foot length (along the wall). This is not right. I must say though that Bowles does a poor job explaining that part (in my opinion). Therefore if you want to simulate a stip load you MUST enter a large “Y” dimension so that the program realizes the effect of a STRIP load and not an AREA load. This should really be built into the worksheet but is not yet.

Attached is a hand calc comparison between the “integrated” and discretized approach.
Boussinesq Integrated vs Discretized
Elastic Method – Compare Integrated to Discretized

Elastic Methods Nomenclature Notes

Elastic Methods Spangler Derives Integrated Method
Offset Surcharge Strip Load Comparison Spreadsheet

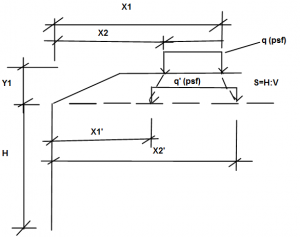
Another problem when using elastic methods is that all equations assume that the load is applied at the same elevation as the top of the wall. How can we handle a slope atop the wall with a load applied at the top of the slope? Well the railroad design manuals (See UPRR Shoring Manual) distribute the load down through the soil at a certain angle (they use a 2V:1H) and find a new uniform load applied at this elevation.