Stability – AISC’s Direct Analysis Method
Intro
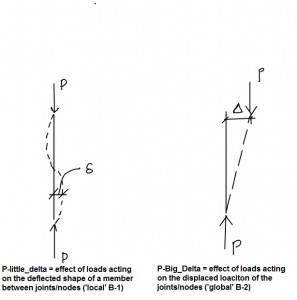
In the 14th Edition of the American Steel Construction Manual the Direct Analysis Method (DAM) is moved into the main specification from the appendix. I know many are not used to this new approach and some will say that if it’s not broke don’t fix it but I like the DA Method. Like anything else you need to put some time into learning it but it’s really not so bad in the end. It is a very interesting approach in that most design codes / manuals do not get into the analysis meaning that they don’t tell you how to get the required/design forces but rather they give an allowable/capacity of the member to which you are designing. However in DAM, AISC is assisting you in your analysis to make the design simpler. Essentially we need to address two different types of deflection/deformation associated with axial load that amplify moments in the structure. The first is P-δ (I may refer to this as P-d) which are moments associated with the axial load and deflection due to column curvature (Think of these as local displacements). The second is P-Δ (I may refer to this as P-D) moments which are caused by axial load and the translation of the end of the column (i.e. interstory drift) think of these as global displacements. Neither of these moments will show up in a first order elastic analysis. Well they may…sorta. I don’t want to get off track so I will explain what I mean later (this refers to common FEM models and placing multiple nodes along a member). We will now cover the DAM for a computer based approach and a simplified hand method.
Overview
The direct analysis method is basically accounting for (3) issues:
- Effects of initial geometric imperfections
- Second-Order effects – Axial-Displacement Moments P-D and P-d (as shown above).
- Effects of material non-linearity – In-elasticity due to residual stresses.
AISC actually states that there are (5) requirements. Below these requirements are listed and how they are addressed (AISC C-C1.1).
Considerations:
- Consider all deformations
- Note that this says ‘consider’ not necessarily include, i.e. column shears deformation, in-plane ‘rigid’ diaphragm displacement.
- The model or analysis shall ‘consider’ all deformations.
- Consider P-d and P-D
- Perform a rigerous second order analysis
- Use B1, B2 Method
- Consider geometric imperfections
- This typically this stems from column out of plumbness
- This may be directly modeled in the analysis
- A notional load may be applied to the analysis
- Use KL = L
- Consider stiffness due to inelasticity. This is typically due to residual stresses in framing members. Therefore some elements may soften ‘inelastically’ prior to reaching their design strength.
- Apply a stiffness reduction factor
- Use KL = L
- Consider uncertainty in strength and stiffness
- Apply a stiffness reduction factor.
- Use KL = L
Applying the Direct Analysis Method
First we will look at applying this method in a strict sense and assuming the use of a computer model. Then we will get to a more conservative hand calc method.
- Model your structure and apply all loads. Set up your load combinations according to LRFD or ASD (Most likely see IBC load combo’s).
- Run a first-order analysis and determine deflections.
- Amplify the ASD loads x 1.6
- Modify the stiffness of all members. For a first trial run use a 0.8 factor. This would be applied to axial (0.8*EA) and flexural (0.8EI) stiffness.
- AISC states that the stiffness reduction need only be applied to members that contribute to the stability of the structure however they can be applied to all members to prevent artificial distortion.
- Run a second-order analysis.
- Amplify the ASD loads x 1.6
- Modify the stiffness of all members. For a first trial run use a 0.8 factor. This would be applied to axial (0.8*EA) and flexural (0.8EI) stiffness.
- AISC states that the stiffness reduction need only be applied to members that contribute to the stability of the structure however they can be applied to all members to prevent artificial distortion.
- So this is just a mouse click away right? Well not quite. You should really know what your analysis software is doing. It is difficult if not impossible in some situations for software programs to perform a rigorous second-order analysis. For the program to perform this analysis it usually needs to run an iterative process on many nodes which may not be realistic. Therefore the program may use a geometric stiffness method which only accounts for P-D moments. Therefore P-d moments are still unaccounted for. However these moments may be “semi” captured if the column element is broken into several nodes. This way the deflection between nodes is captured in the analysis. AISC recognizes this practical problem and states that the P-d effects on the structure may be neglected if the second order drift to first order drift ratio (also known as B2) is equal or less than 1.7, also no more than 1/3 of the total gravity load on the structure is supported by columns that are part of the moment-resisting frames in the direction of translation being considered.
- In the commentary they equate the 1.7 to a 1.5 limit with no stiffness reduction.
- Furthermore P-d effects must be considered to individual members subject to compression and flexure. In this case B-1 could be used.
- Find the drift ratio (B2) of second order to first order drift. This will be used to determine what sort of notional loads will need to be applied.
- Notional loads – Initial Imperfections
- Initial imperfections may be directly applied in the model. Typically an out of plumbness of 1/500 is used the maximum specified in the Code of Standard Practice.
- If not modeled directly notional loads may be applied. These are lateral loads Ni =0.002*α*Yi. These loads are distributed over the level in the same maner as the gravity load.
- Ni = notional load at level i
- α = 1.0 (LRFD); α = 1.6 (ASD)
- Yi = gravity load applied at level i under each respective load combination
- If B2 (drift ratio) is <= 1.7 then the notional loads may be applied as a minimum. Meaning that they are applied to gravity only load combinations but are not applied if the ‘actual’ lateral loads i.e. wind/EQ forces are greater than the notional load.
- Adjust stiffness
- For all stiffness that contribute to the stability of the structure a 0.8 factor shall be applied i.e. EI, AE, etc.
- Additionally for flexure the stiffness should be multiplied by 0.8
:
- For
- For
- α = 1.0 (LRFD); α = 1.6 (ASD)
- Pr = required axial compressive strength of the member
- Py = axial yield strength = Fy*Ag (yield stress x gross area)
- For
- In lieu of using taub a notional load of 0.001*α*Yi may be applied to the structure in similar fashion as the notional loads for initial imperfections. However these notional loads are additive for all load combinations.
- Rerun second order analysis and check drift ratio, B2. Update any parameters based on the new drift ratio.
- Design members using K=1. No Alignment Chart Required, Yeah!!!
Applying the Direct Analysis Method
Now for a simplified hand calc to demonstrate the use of B1 and B2.
This post got to be a tad long so I’m going to break this into a separate post here.
References:
AISC 14th Edition CSC’s “Simple Guide to Direct Analysis” and webinar. Note that CSC’s Fastrak software does perform a rigorous second order analysis. RISA’s Practical Analysis with the AISC 13th Edition by Josh Plummer AISC Engineering Journal 3th Q 2008 “A comparison of Frame Stability Analysis Methods”
I am designing a three tier pipe rack by direct analysis method in Risa 3D using AISC 13th edition. Is it compulsory to apply notional loads when we are using direct analysis.
The short answer – yes, notional loads should be applied for all load combinations. However –
If the ratio of the second order drift to first order drift (referred to as B2 in the approximate second order method) is less than 1.5 (or less than 1.7 if you are running the analysis using the reduced stiffness) than the notional loads may be applied as minimums. Meaning – for load combinations that have lateral forces (i.e. wind and seismic) if the lateral force due to wind/seismic is greater than the notional load then the notional load does not need to be applied. However if the load combination does not include any lateral forces (no wind/seismic) than the notional load should be applied.
If the drift ratio is greater than 1.5 than you must apply the notional load as additive to all load cases in the same direction as the lateral force (i.e. worst case).
Actually, how do we reduce the stiffness about 20% in structural analysis software? If we adjust E or A (E or I), then the required strength will be correctly adjusted following the modified stiffness. But how about the available strength? If we adjust E or A (E or I), then the available strength will be wrong.
That is a good point. Some software packages have the direct analysis method built in, however if it is not I suppose you could use the reduced E in your member design. Or manually determine the member capacity. Or even have two models. Actually you may need two models anyway or atleast run the model twice as you would not check the drift requirements using the reduced stiffness.
Here http://communities.bentley.com/products/structural/structural_analysis___design/w/structural_analysis_and_design__wiki/6011.asce-7-aisc-360-and-the-direct-analysis-method-in-the-ram-structural-system.aspx
Is one software that walks through the DAM. RISA is another one that has this option and I’m sure there are many more.
Thanks for your kind explanation.
In addition, regarding P-d (small d) effect, you mentioned that the moment may be “semi” captured if the column element is broken into several nodes.
I agree that the P-d moment may be added, but in that case there is a problem. Many software automatically calculate whether the AISC’s requirements are satisfied or not, and it is broadly called as ‘Code Check’.
If, like you said, the element is divided with some parts using additional nodes, the software performs code check along the divided length. So the unbraced length will be shorter than the original one and it causes wrong results. In this case, I think, the only way to solve the problem is to input the unbraced length manually.
Could it also be controlled easily in software?